CBI Colloquium “Non-Linear Super-Stencils for Turbulence Model Corrections” (Prof. Patrick Jenny, ETH Zürich)

Accurate simulation of turbulent flows remains a challenge due to the high computational cost of direct numerical simulations (DNS) and the limitations of traditional turbulence models. This research explores a novel approach to augmenting standard models for Reynolds-Averaged Navier-Stokes (RANS) simulations using a Non-Linear Super-Stencil (NLSS). The proposed method introduces a fully connected neural network that learns a mapping from the local mean flow field to a corrective force term, which is added to a standard RANS solver in order to align its solution with high-fidelity data; an illustration of an NLSS is shown in Fig. 1.

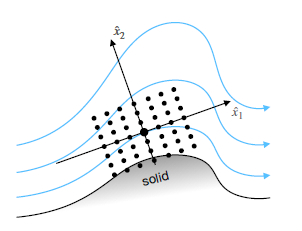
Figure 1: Non-Linear Super-Stencil (black dots): The stencil is centered around the point at which the correction force shall be determined, and it is aligned with the mean velocity at its center.

A procedure is devised to extract training data from reference DNS and large eddy simulations (LES). To reduce the complexity of the non-linear mapping, the dimensionless local flow data is aligned with the local mean velocity, and the local support domain is scaled by the turbulent integral length scale. After being trained on a single periodic hill case, the NLSS-corrected RANS solver is shown to generalize to different periodic hill geometries and different Reynolds numbers, producing significantly more accurate solutions than the uncorrected RANS simulations. For demonstration, Fig. 2 shows RANS simulation results with and without NLSS-correction along with high fidelity references (mean velocity profiles in the top plots and wall shear stresses on the bottom) of two test cases which were not used for training. For training a domain of lenth L = 9m, a hill stretch factor of alpha = 1 and a Reynolds number of Re = 10595 were considered, while L = 13:929m, alpha = 1:5 and Re = 5600 were chosen for the left test case and L = 9m, alpha = 1 and Re = 19000 for right test case. For both test cases it can be observed that the NLSS-corrected RANS solutions closely agree with the reference data (much better than the uncorrected ones), thus demonstrating the ability of the NLSS to generalize across different geometries and Reynolds numbers.

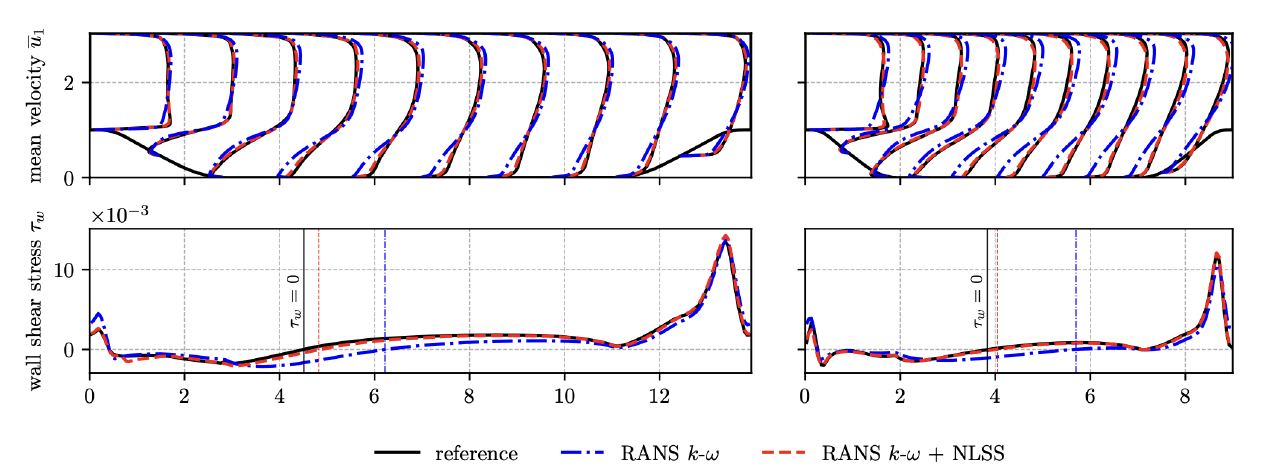
Figure 2: Generalization: RANS simulation results of two test cases (which were not used for training) with and without NLSS-correction along with high fidelity data. Shown on the top are profiles of the horizontal mean velocity component at ten different downstream locations, and on the bottom the wall shear stresses along the bottom wall of the periodic hill geometries. Locations of mean flow re-attachment of reference and NLSS-corrected solutions are marked by the vertical lines.

While the ability of NLSS for model correction is demonstrated here for turbulent flows, the concept is more general and will be explored in the future for other systems of partial differential equations involving physical models.